Sistemi complessi

La ricerca svolta presso DFA si  focalizza nella descrizione matematica dell'architettura e della dinamica dei sistemi complessi. L'obiettivo principale è capire come un sistema complesso, ovvero un sistema composto da tanti elementi in interazione fra loro in maniera nonlineare,  si auto-organizza dando origine a  vari comportamenti collettivi. I metodi utilizzati sono strumenti matematici della teoria dei grafi, della meccanica statistica, della dinamica non lineare e delle simulazioni numeriche su larga scala. Le applicazioni spaziano dalla biologia ai sistemi socio-economici, comprese le reti create dall'uomo, in cui vengono affrontati sia i problemi fondamentali che la ricerca applicata in collaborazione con aziende private. Nel 2021 il fisico italiano Giorgio Parisi ha ricevuto il premio Nobel per la Fisica per le sue pioneristiche ricerche sui sistemi complessi.

Meccanica statistica

Docenti: Vito Latora, Alessandro Pluchino, Andrea Rapisarda
La meccanica statistica è un potente formalismo fisico-matematico grazie al quale si riesce a spiegare la connessione fra il comportamento termodinamico macroscopico di un sistema e la dinamica microscopica dei suoi componenti elementari e che ha avuto un enorme successo per i sistemi all’equilibrio.  Negli ultimi 25 anni l’attenzione si è spostata sui sistemi lontano dall’equilibrio e con interazioni a lungo raggio per i quali il formalismo  della meccanica statistica standard non funziona. Uno degli approcci più di successo in questa direzione è la meccanica statistica nonestensiva introdotta nel 1988 dal fisico Constantino Tsallis. All’interno del DFA lavoriamo da anni  su questa teoria con applicazioni che vanno dai terremoti alle reti complesse.

Reti complesse

Docenti: Vito Latora, Alessandro Pluchino, Andrea Rapisarda
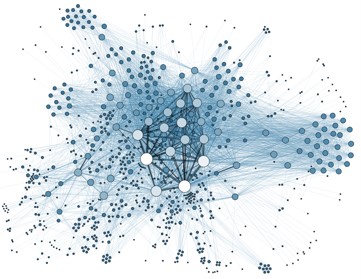
Molti sistemi complessi del mondo reale possono essere modellizzati come reti di unità dinamiche accoppiate. Al DFA studiamo sia l'architettura che la dinamica di reti complesse con l'obiettivo principale di comprendere come la topologia del grafo sottostante influenzi la dinamica di un sistema e l'emergere di comportamenti collettivi. Gli argomenti trattati includono reti spaziali e temporali, reti con molti strati ed anche reti di ordine superiore come i complessi simpliciali.

Dinamica non lineare e caos

Docenti: Vito Latora, Alessandro Pluchino, Andrea Rapisarda
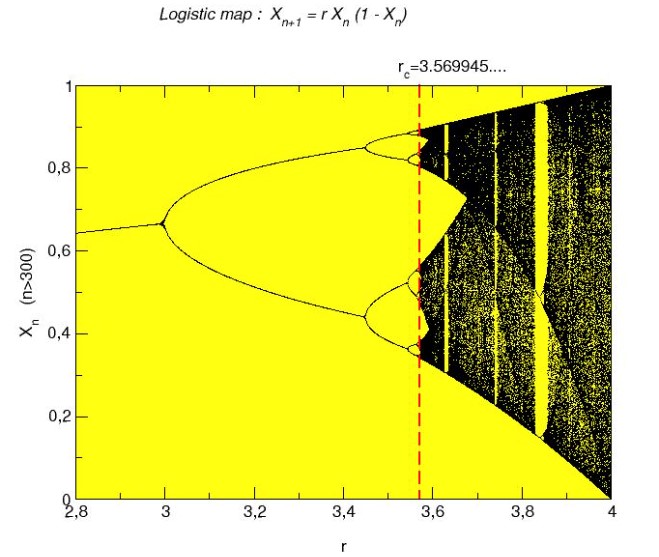
Il caos e la dinamica non lineare rappresentano fonti inesauribili di concetti e tecniche per lo sviluppo di modelli di sistemi complessi. Ad esempio, è stato scoperto che molti sistemi complessi – tra cui il nostro cervello, le reti socio-economiche globali, il clima planetario e molti altri – si portano spontaneamente al “bordo del caos”, una sorta di regime  in cui si possono osservare   eventi di qualsiasi dimensione  e durata temporale descritti da leggi a potenza.

Applicazioni interdisciplinari

Docenti: Vito Latora, Alessandro Pluchino, Andrea Rapisarda
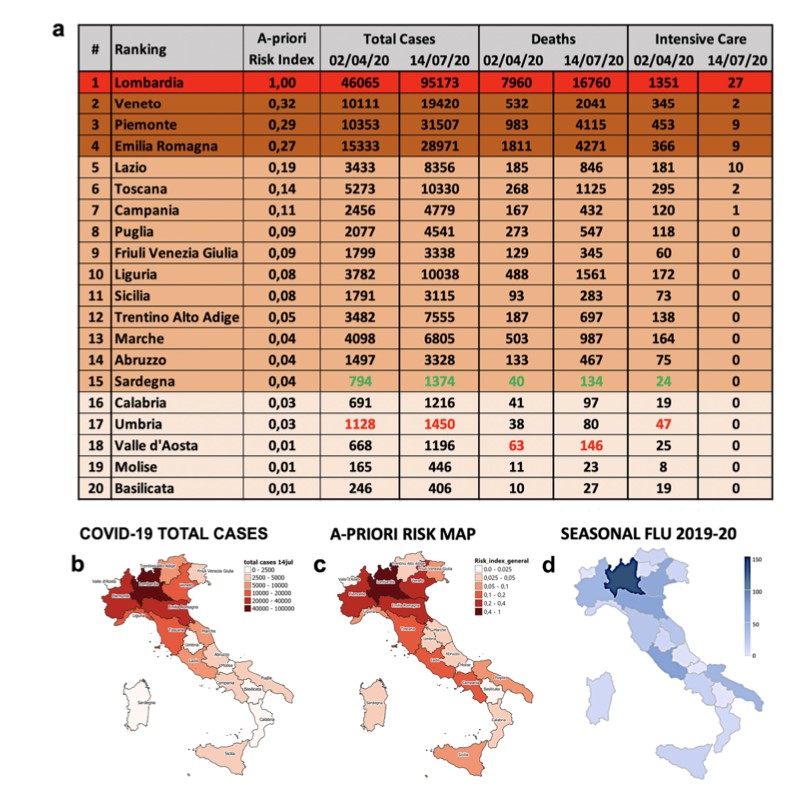
Analisi di reti complesse, modelli basati su agenti interagenti, tecniche di apprendimento automatico e molti altri strumenti statistici ci consentono di affrontare oggi molti diversi sistemi complessi, seguendo un approccio interdisciplinare integrato. Le applicazioni alle reti sociali ed ecologiche, le dinamiche dei terremoti, la diffusione di epidemie, i mercati finanziari, le dinamiche cerebrali e l'intelligenza artificiale sono solo esempi dei numerosi studi di ricerca condotti presso il DFA. Diversi studi sono stati pure fatti per capire la pandemia da Covid-19.